Медиана към хипотенуза в правоъгълен триъгълник 7 клас

📞 Онлайн уроци по математика за цялата страна◆ гл.ас. д-р Атанас Илчев◆ Индивидуални и групови уроци • Тел: 0883 375 433◆ ISEE Upper Level • Подготовка за американски колеж◆ 📞 Онлайн уроци по математика за цялата страна◆ гл.ас. д-р Атанас Илчев◆ Индивидуални и групови уроци • Тел: 0883 375 433◆ ISEE Upper Level • Подготовка за американски колеж◆

Математика › 7 клас › Геометрия › Медиана към хипотенузата

Медиана към хипотенузата в правоъгълен триъгълник
Теореми и задачи

Пълен урок с теореми, решени задачи с доказателства, самостоятелна работа и интерактивен тест

7 клас 2 теореми 2 разработени задачи 15 въпроса тест Д-р Атанас Илчев

Медианата към хипотенузата е равна на половината от хипотенузата — теореми, доказателства и задачи за 7 клас

В правоъгълния триъгълник медианата към хипотенузата има изключително важно свойство: тя е равна на половината от хипотенузата. Това твърдение се използва често в числови задачи, доказателства, свързани с равностранни и равнобедрени триъгълници, средни точки и периметри.

Теория

Теорема 1: Медианата към хипотенузата в правоъгълен триъгълник е равна на половината от хипотенузата.

Теорема 2 (обратна): Ако в \(\triangle ABC\) медианата \(CM\) (\(M\in AB\)) е равна на половината от страната \(AB\), то триъгълникът е правоъгълен с прав ъгъл при \(C\).

Полезна идея: В много задачи Теорема 1 се комбинира с теоремата за ъгъл \(30°\) — ако медианата е равна на катет, триъгълникът \(AMC\) е равностранен и ъгълът при основата е \(60°\), а срещулежащият е \(30°\).

---

Разработени задачи

Кликнете върху задача, за да видите решението.

1

В правоъгълния \(\triangle ABC\) медианата към хипотенузата \(AB\) е равна на катета \(AC\) и \(CD\) (\(D\in AB\)) е височина. а) Намерете \(AC\), ако \(AB=8\) cm. б) Ако \(BC=a\) cm, намерете \(CD\). в) Ако \(P\) и \(Q\) са средите на катетите \(AC\) и \(BC\), докажете, че периметърът на \(\triangle ABC\) е два пъти по-голям от периметъра на \(\triangle PDQ\).

▼

Решение

а) Намерете AC при AB=8 cm

От Теорема 1: \(CM=\dfrac{AB}{2}=4\) cm. Тъй като по условие \(CM=AC\), следва \(AC=4\) cm.

б) Намерете CD при BC=a cm

Тъй като \(CM=AC=AM=4\) cm (от Теорема 1 \(CM=AM\)), триъгълникът \(AMC\) е равностранен, следователно \(\sphericalangle BAC=60°\) и \(\sphericalangle ABC=30°\).

В \(\triangle BDC\): \(\sphericalangle BDC=90°\) и \(\sphericalangle DBC=30°\). От теоремата за ъгъл \(30°\): \[CD=\frac{BC}{2}=\frac{a}{2}\ \text{cm}.\]

в) Доказателство за периметрите

Нека \(BC=a\), \(AC=b\), \(AB=c\). Тъй като \(P\) е среда на \(AC\), то \(DP\) е медиана към хипотенузата в правоъгълния \(\triangle ADC\), следователно \(PD=\dfrac{AC}{2}=\dfrac{b}{2}\). Аналогично \(DQ=\dfrac{BC}{2}=\dfrac{a}{2}\).

Тъй като \(PC=PD\) и \(QC=QD\), точките \(P\) и \(Q\) лежат на симетралата на \(CD\), следователно \(PQ\perp CD\). От \(CD\perp AB\) и \(CD\perp PQ\) получаваме \(PQ\parallel AB\).

От \(PQ\parallel AB\): \(\sphericalangle PQC=\sphericalangle ABC=30°\). В правоъгълния \(\triangle PQC\) с ъгъл \(30°\): \[PC=\frac{PQ}{2} \;\Rightarrow\; PQ=2PC=2\cdot\frac{b}{4}=\frac{b}{2}\cdot\frac{AB}{b}\cdot\frac{b}{2}=\frac{c}{2}.\] По-директно: \(PQ\parallel AB\) и \(P,Q\) са средни точки на \(AC,BC\) — от теоремата за средната линия \(PQ=\dfrac{c}{2}\).

Следователно: \[P_{\triangle PDQ}=PD+DQ+PQ=\frac{b}{2}+\frac{a}{2}+\frac{c}{2}=\frac{a+b+c}{2}=\frac{P_{\triangle ABC}}{2}.\ \blacksquare\]

2

За квадрата \(ABCD\) точката \(K\) е среда на \(AD\) и \(BH\) е перпендикулярът от \(B\) към \(KC\) (\(H\in KC\)). Ако \(AH=6\) cm, намерете лицето на квадрата \(ABCD\).

▼

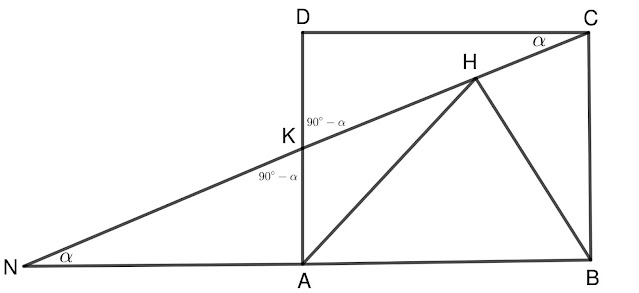
Решение Нека продължението на \(KC\) пресича продължението на \(AB\) в точка \(N\). Нека \(\sphericalangle KCD=\alpha\), следователно \(\sphericalangle DKC=90°-\alpha\). Ъглите \(\sphericalangle DKC\) и \(\sphericalangle NKA\) са връхни, следователно \(\sphericalangle NKA=90°-\alpha\) и \(\sphericalangle KNA=\alpha\).

Разглеждаме \(\triangle KNA\) и \(\triangle KCD\):
1) \(KA=KD\) — \(K\) е среда на \(AD\)
2) \(\sphericalangle NKA=\sphericalangle DKC\) — връхни ъгли
3) \(\sphericalangle NAK=\sphericalangle CDK=90°\)
Следователно \(\triangle KNA\cong\triangle KCD\) по втори признак, откъдето \(NA=CD=AB\), т.е. \(A\) е среда на \(NB\).

Тъй като \(\sphericalangle NHB=90°\) (дадено) и \(A\) е среда на хипотенузата \(NB\) на правоъгълния \(\triangle NHB\), то по Теорема 1: \[HA=\frac{NB}{2}=\frac{2AB}{2}=AB.\] Следователно \(AB=HA=6\) cm и \[S_{ABCD}=AB^2=36\ \text{cm}^2.\]

---

Задачи за самостоятелна работа

Задача 1Даден е правоъгълен \(\triangle ABC\) с \(\sphericalangle C=90°\), \(\sphericalangle A=15°\) и лице \(S=72\) cm². Намерете дължината на хипотенузата \(AB\) и на височината \(CD\) към нея.

Задача 2В остроъгълния \(\triangle ABC\) са построени височините \(AH\) и \(CD\), пресичащи се в \(O\). Точката \(P\) е среда на \(AB\), а \(M\) — среда на \(OC\). Намерете \(\sphericalangle PHM\).

Задача 3В правоъгълния \(\triangle ABC\) (\(\sphericalangle C=90°\)) са построени: височина \(CH\) (\(H\in AB\)), ъглополовяща \(BL\) на \(\sphericalangle ABC\) (\(L\in AC\)) и ъглополовяща \(CM\) на \(\sphericalangle ACH\) (\(M\in AH\)). Определете вида на \(\triangle MBC\).

Задача 4Даден е правоъгълен \(\triangle ABC\) (\(\alpha>\beta\)). Отсечките \(CH\), \(CL\) и \(CM\) са съответно височина, ъглополовяща и медиана към хипотенузата \(AB\). Докажете, че: а) \(\sphericalangle HCL=\alpha-45°=\dfrac{\alpha-\beta}{2}\); б) \(\sphericalangle HCM=\alpha-\beta\); в) \(\sphericalangle LCM=\dfrac{\alpha-\beta}{2}=\sphericalangle LCH\).

---

Онлайн тест

15 въпроса • 4 точки за верен отговор • максимум 60 точки

Тест: Медиана към хипотенузата в правоъгълен триъгълник

Изберете верния отговор за всеки въпрос, след което натиснете КРАЙ.

1Медианата към хипотенузата в правоъгълен триъгълник е равна на:

хипотенузата половината от хипотенузата сбора от катетите четвъртината от хипотенузата

2Ако медианата \(CM\) в \(\triangle ABC\) е равна на половината от \(AB\), то:

триъгълникът е равностранен триъгълникът е правоъгълен с прав ъгъл при \(C\) триъгълникът е равнобедрен \(AB\) е основа

3В правоъгълен \(\triangle ABC\) медианата към хипотенузата е равна на катета \(AC\) и \(AB=8\) cm. Катетът \(AC\) е равен на:

\(8\) cm \(4\) cm \(2\) cm \(6\) cm

4Ако \(CM=AC=AM\), то \(\triangle AMC\) е:

правоъгълен равностранен равнобедрен тъпоъгълен

5Ако \(\triangle AMC\) е равностранен и \(\sphericalangle ACB=90°\), то \(\sphericalangle ABC\) е равен на:

\(60°\) \(30°\) \(45°\) \(90°\)

6При условията от задача 1 (медиана = катет, \(\sphericalangle ABC=30°\), \(BC=a\)), височината \(CD\) е равна на:

\(a\) \(\dfrac{a}{2}\) \(2a\) \(\dfrac{a}{4}\)

7\(P\) и \(Q\) са средите на катетите \(AC\) и \(BC\). Отсечката \(PQ\) е равна на:

\(AB\) \(\dfrac{AB}{2}\) \(\dfrac{AB}{4}\) \(2\cdot AB\)

8Периметърът на \(\triangle PDQ\) спрямо периметъра на \(\triangle ABC\) е:

равен два пъти по-малък четири пъти по-малък два пъти по-голям

9В задача 2 с квадрат \(ABCD\), \(AH=6\) cm. Лицето на квадрата е:

\(6\) cm² \(36\) cm² \(12\) cm² \(24\) cm²

10В задача 2, еднаквостта \(\triangle KNA\cong\triangle KCD\) е доказана по кой признак?

първи признак втори признак трети признак пряко от определението

11Ако \(CM\) е медиана в \(\triangle ABC\) и \(\sphericalangle ACB=90°\), то \(CM\), \(AM\) и \(BM\) са:

неравни равни помежду си \(CM=2AM\) \(AM=2BM\)

12\(P\) е среда на \(AC\) и \(D\) е пета на височината в правоъгълния \(\triangle ABC\) (\(\sphericalangle C=90°\)). Тогава \(PD\) е равно на:

\(AC\) \(\dfrac{AC}{2}\) \(\dfrac{AB}{2}\) \(CD\)

13В задача 2, след като установим, че \(A\) е среда на \(NB\) и \(\sphericalangle NHB=90°\), то \(HA\) е:

височина в \(\triangle NHB\) медиана към хипотенузата в \(\triangle NHB\) ъглополовяща в \(\triangle NHB\) симетрала на \(NB\)

14\(AB=8\) cm, медианата към \(AB\) е равна на \(AC\) и \(BC=6\) cm. Височината \(CD\) е равна на:

\(4\) cm \(3\) cm \(6\) cm \(2\) cm

15В задача 1в, защо \(PQ\parallel AB\)?

защото \(P\) и \(Q\) са средни точки защото \(CD\perp PQ\) и \(CD\perp AB\), следователно \(PQ\parallel AB\) защото \(PQ=AB/2\) защото \(\sphericalangle PDQ=90°\)

---

Видео урок

Още обяснени и решени задачи, свързани с този урок, можете да намерите в клипа по-долу:

Видео урок — Медиана към хипотенузата в правоъгълен триъгълник

---

Използвана литература

1. 1.Сборник за 7 клас, П. Рангелова и др., Коала Прес, Пловдив, 2020
2. 2.Тест Математика 7 клас, Д. Гълъбова и др., Веди, София, 2020
3. 3.Сборник задачи по математика за 7 клас, М. Лилкова и др., Просвета, София
4. 4.Книга за ученика за 7 клас, З. Паскалева и др., Архимед, София, 2018
5. 5.Текуща подготовка по математика за НВО в 7 клас, Б. Савова и др., Просвета, 2020
6. 6.Нови пробни изпити за НВО след 7 клас, Регалия 6, 2015
7. 7.Тестове по математика, Л. Любенов, Ц. Байчева, изд. DOMINO, 2017
8. 8.Нови тематични тестове за 7 клас, М. Рангелова, Коала Прес, 2008
9. 9.Учебно помагало за ЗИП по математика за 7 клас, И. Тонов, Т. Тонова, Просвета, 2011
10. 10.Тестове по математика за 7 клас, Л. Дилкина, К. Бекриев, Коала Прес, 2014
11. 11.Сборник контролни работи и тестове, П. Рангелова, Коала Прес, 2009
12. 12.Сп. Математика; Сп. Математика+

Запишете урок

Индивидуални и групови онлайн уроци по математика за цялата страна

🎓 Подготовка за изпити

• ›НВО по математика след 7 клас
• ›НВО по математика след 10 клас
• ›Кандидатстудентски изпити по математика
• ›Прием в университети в чужбина (ISEE, SAT, A-Level)

📚 Текущо обучение и студенти

• ›Усвояване на текущия учебен материал (всички класове)
• ›Студенти: Мат. анализ, Линейна алгебра, Аналитична геометрия, Диф. уравнения, Теория на вероятностите, Статистика и др.

✆ 0883 375 433 ☎ Viber

Харесва ли ви съдържанието?

Ако този урок ви е бил полезен, можете да подкрепите създаването на нови безплатни материали.

📞 Онлайн уроци по математика за цялата страна◆ гл.ас. д-р Атанас Илчев◆ Индивидуални и групови уроци • Тел: 0883 375 433◆ ISEE Upper Level • Подготовка за американски колеж◆ 📞 Онлайн уроци по математика за цялата страна◆ гл.ас. д-р Атанас Илчев◆ Индивидуални и групови уроци • Тел: 0883 375 433◆ ISEE Upper Level • Подготовка за американски колеж◆