Трети признак за еднаквост на триъгълници 7 клас

Теорема 1 (III признак за еднаквост): Ако страните на един триъгълник са съответно равни на страните на друг триъгълник, то двата триъгълника са еднакви.

1 Задача: Отсечките $BD$ и $B_1D_1$ са медиани съответно в $\triangle ABC$ и $\triangle A_1B_1C_1$. Докажете, че ако $AC=A_1C_1$ и $BD=B_1D_1$ и $\sphericalangle ADB=\sphericalangle A_1D_1B_1$, то триъгълниците $ABC$ и $A_1B_1C_1$ са еднакви.

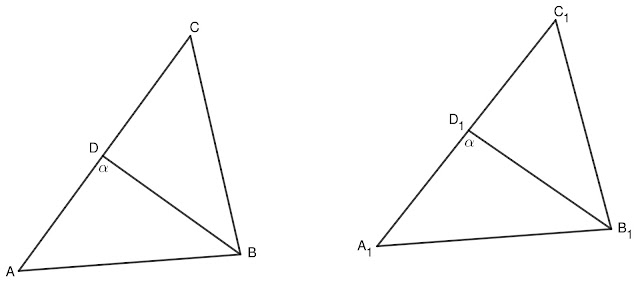
Решение: Тъй като $AC=A_1C_1$ и $BD$, $B_1D_1$ са медиани следва, че (1) $AD=DC=A_1D_1=D_1C_1$.

Разглеждаме $\triangle ABD$ и $\triangle A_1B_1D_1$:

1) $\sphericalangle ADB=\sphericalangle A_1D_1B_1$ (по условие);

2) $AD=A_1D_1$ (от (1));

3) $BD=B_1D_1$ (по условие),

Следователно $\triangle ABD\cong\triangle A_1B_1D_1$ по I признак. Оттук (2) $AB=A_1B_1$.

От $\sphericalangle ADB=\sphericalangle A_1D_1B_1=\alpha$ следва, че (3) $\sphericalangle BDC=\sphericalangle B_1D_1C_1=180^{\circ}-\alpha$.

Разглеждаме $\triangle BDC$ и $\triangle B_1D_1C_1$:

1) $BD=B_1D_1$ (по условие);

2) $CD=C_1D_1$ (от (1));

3) $\sphericalangle BDC=\sphericalangle B_1D_1C_1$ (от (3)),

Следователно $\triangle BDC\cong\triangle B_1D_1C_1$ по I признак. Оттук (4) $BC=B_1C_1$.

Разглеждаме $\triangle ABC$ и $\triangle A_1B_1C_1$:

1) $AB=A_1B_1$ (от (2));

2) $BC=B_1C_1$ (от (4));

3) $AC=A_1C_1$ (по условие),

Следователно $\triangle ABC\cong\triangle A_1B_1C_1$ по III признак.

2 Задача: Докажете, че ако два триъгълника са равнолицеви и трите височини на единия триъгълник са съответно равни на трите височини на другия триъгълник, то двата триъгълника са еднакви.

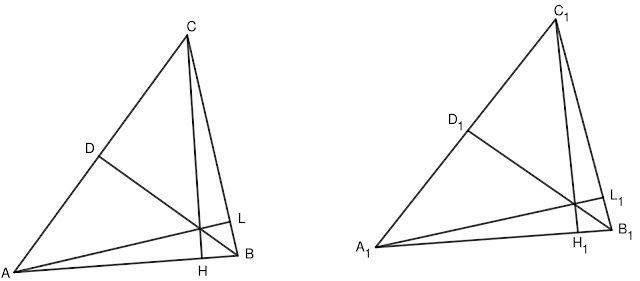
Решение: Нека $AL$, $BD$ и $CH$ са височините в $\triangle ABC$ и $A_1L_1$, $B_1D_1$ и $C_1H_1$ са височините в $\triangle A_1B_1C_1$. По условие $AL=A_1L_1$, $BD=B_1D_1$ и $CH=C_1H_1$, и $S_{\triangle ABC}=S_{\triangle A_1B_1C_1}$.

Лицето на триъгълник е:

$S_{\triangle ABC}=\frac{AB\cdot CH}{2}=\frac{BC\cdot AL}{2}=\frac{AC\cdot BD}{2}$

$S_{\triangle A_1B_1C_1}=\frac{A_1B_1\cdot C_1H_1}{2}=\frac{B_1C_1\cdot A_1L_1}{2}=\frac{A_1C_1\cdot B_1D_1}{2}$

От равенствата:

(1) $\frac{AB\cdot CH}{2}=\frac{A_1B_1\cdot C_1H_1}{2}$ и $CH=C_1H_1$ $\implies$ $AB=A_1B_1$

(2) $\frac{BC\cdot AL}{2}=\frac{B_1C_1\cdot A_1L_1}{2}$ и $AL=A_1L_1$ $\implies$ $BC=B_1C_1$

(3) $\frac{AC\cdot BD}{2}=\frac{A_1C_1\cdot B_1D_1}{2}$ и $BD=B_1D_1$ $\implies$ $AC=A_1C_1$

Разглеждаме $\triangle ABC$ и $\triangle A_1B_1C_1$:

1) $AB=A_1B_1$ (от (1));

2) $BC=B_1C_1$ (от (2));

3) $AC=A_1C_1$ (от (3)),

Следователно $\triangle ABC\cong\triangle A_1B_1C_1$ по III признак.

Задачи за самостоятелна работа

1. Точките $C$ и $D$ от симетралата на отсечката $AB$ са от една и съща страна на $AB$. Известно е и че $AD^{\rightarrow}\cap BC^{\rightarrow}=E$ и $AC^{\rightarrow}\cap BD^{\rightarrow}=F$. Докажете, че $\sphericalangle CAE=\sphericalangle CBF$.

2. За $\triangle ABC$ и $\triangle A_1B_1C_1$ е дадено, че медианите $CM$ и $C_1M_1$ са равни. Ако $AB=A_1B_1$ и $AC=A_1C_1$, докажете, че:

а) $\triangle AMC\cong\triangle A_1M_1C_1$; б) $\triangle ABC\cong\triangle A_1B_1C_1$.

3. Докажете, че два равнобедрени триъгълника са еднакви, ако бедро и медиана към него от единия триъгълник са съответно равни на бедро и медиана към него от другия триъгълник.

4. Докажете, че два триъгълника са еднакви, ако имат по две страни и медиани, излизащи от един и същи връх, съответно равни.

Видео уроци

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +